1. Introduction
Current trends of the increasing complexity of AI workloads have driven the interest in dedicated processors for AI applications. Since current technology is no longer able to double the processing speed with every new silicon generation at a constant power, due to the slow-down of Moore’s law and Dennard scaling, today’s AI processors and accelerators need to make more efficient use of the available power.
As the model and dataset sizes of deep learning applications continue to increase, the scalability of machine learning systems becomes indispensable, in order to cope with the considerable compute requirements of these applications. Training large distributed models, however, creates several challenges. It relies on the effective use of the available compute, memory, and networking resources shared among the different nodes, and limited by the available power budget.
The choice of computer arithmetic is an important part in any accelerator or processor design, as it has a direct impact on hardware complexity and compute efficiency, as well as memory and communication bandwidth utilization. For these reasons, the use of efficient numerical representations is of critical importance, since it allows increased power efficiency due to the improved compute throughput and improved utilization of the communication bandwidth.
2. Floating-point number representations
Many scientific computations requiring a high level of numeric precision rely on the IEEE 754 standard for floating-point arithmetic. This defines floating-point encodings for approximate representations of real numbers, and the arithmetic defined on such numbers. Indeed, many scientific applications use the universal IEEE 754 32-bit and 64-bit floating-point representations as the default implementation to deliver high throughput and high numeric-precision workloads.
However, in machine intelligence applications, which make extensive use of tensor linear algebra, the use of more efficient floating-point representations, for training and inference purposes, has become the industry standard. Many machine intelligence processors offer competing forms of 16-bit floating-point numerical representation to accelerate machine intelligence workloads, such as the IEEE 754 half-precision 16-bit floating point numbers or the Google bfloat16 format. These are often combined with the use of a higher-precision accumulator to offset the reduction in range and precision when using lower-precision input values.
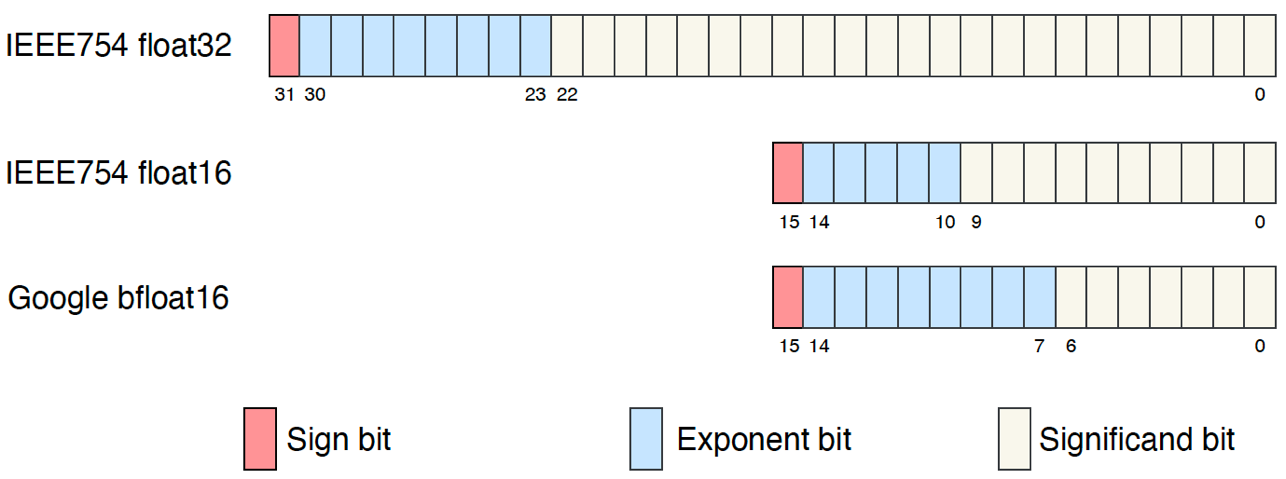
Fig. 2.1 16-bit floating-point formats for machine learning
3. The IPU 16-bit floating point format
Conceived to tackle the complexity of machine intelligence workloads, the IPU’s hardware and software architectures provide the user with the means to realize fast and efficient training and inference of their deep learning models using lower precision arithmetic. The Graphcore Mk2 Colossus IPU architecture currently defines floating-point representations and arithmetic operations which use IEEE 754 32- and 16-bit representations
This whitepaper will provide an overview of the different architectural and algorithmic choices for the efficient use of mixed precision in machine intelligence computations using the IPU.
4. Lower precision for higher power efficiency
Historically, the training of state-of-the-art deep neural network models has relied on IEEE 754 single-precision 32-bit floating-point arithmetic. However, for machine intelligence applications more efficient implementations based on half-precision or 16-bit floating-point have been typically employed, using mixed precision multiply-accumulate operations with 16-bit floating-point (FP16) multiplicands and 32-bit floating-point (FP32) accumulation.
When reducing the numerical precision of a floating-point representation, the designer is often faced with the trade-off between offering the user more range or more precision. As a result, the choice of a suitable exponent/significand split has many hardware implications, in terms of area and power consumption, and may lead to an irrecoverably degraded performance, unless the hardware, software and algorithms are designed to overcome the inherent limitations of using more efficient numerical representations.
Reducing precision for efficient data representation in deep learning offers several benefits. Firstly, low precision arithmetic has motivated recent innovations in processor design as it allows faster compute for training and inference. In practice, existing hardware resources, such as multipliers, are reused to deliver higher throughputs (FLOPs per cycle). For instance, four FP16 multiplications (4 FLOPs) per cycle can be executed using the same hardware which is required for a single FP32 multiplication, which translates to higher throughputs and a better power efficiency per operation.
Secondly, in addition to increasing the compute throughput with small precision, as the data size decreases, the available memory can be used to fit larger models or use larger batch sizes.
Finally, in the context of distributed systems, the available transfer bandwidth can be used to exchange more data for the same power consumption.
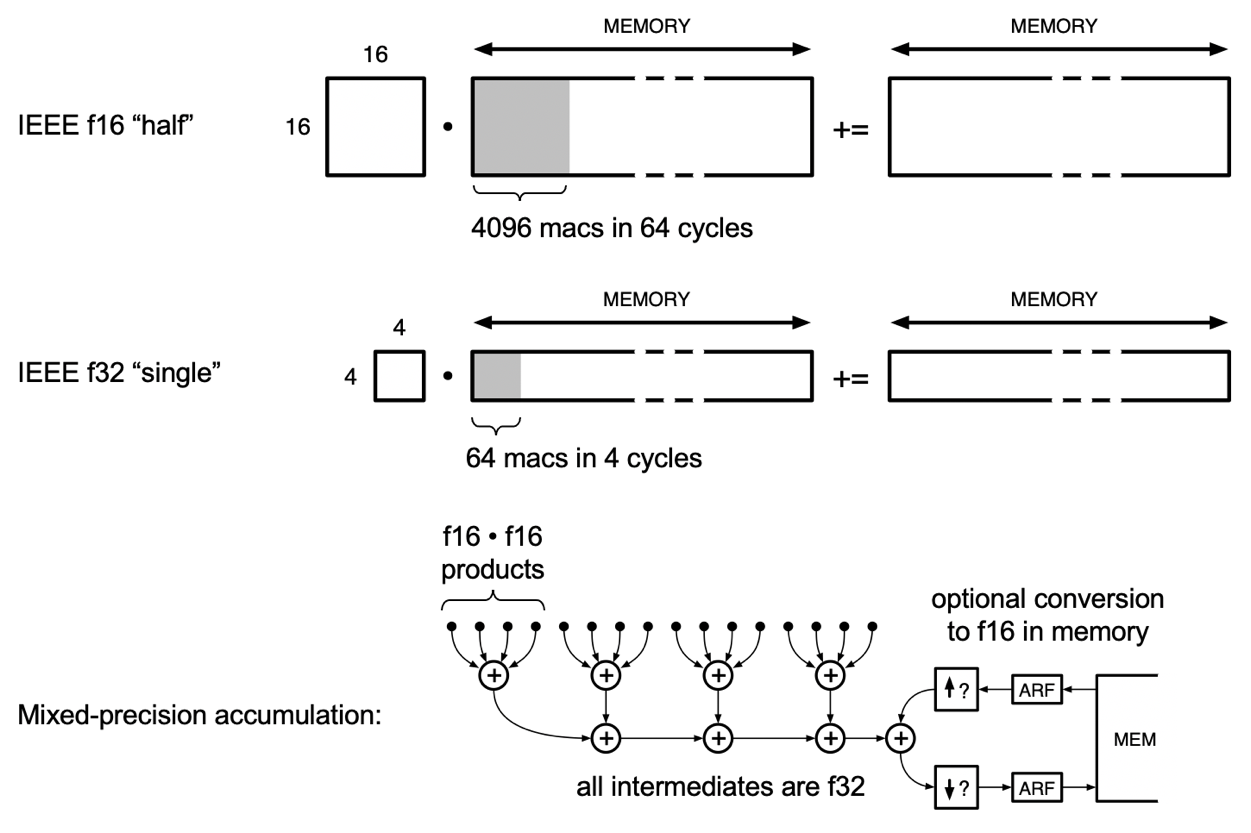
Fig. 4.1 Streaming matmuls on the Colossus Mk2
5. Mixed-precision arithmetic
The Colossus IPU architecture provides a wide range of mixed-precision operations that take FP16 non-accumulator operands, and form results in FP32 accumulators, which may then optionally be delivered as FP16. These operations can be divided into vector operations(such as the vector sum of elements, sum of absolutes and sum of squares) and dot products.
Dot-product operations constitute an elemental building block in all deep-learning models, from computing norms and cosine similarities, to matrix products, and different forms of convolutions. Indeed, improving the computational efficiency of these operations embodies the very function of deep learning processors and accelerators. To facilitate the execution of lower precision general matrix multiplications (GEMMs), the Colossus IPU’s Accumulating Matrix Product (AMP) and Slim Convolution (SLIC) instructions deliver high performance multiply-accumulate sequences and are supported for both single-precision and half-precision number formats and operate in the same basic manner.
To make use of the fine-grained parallelism in the IPU architecture, the IPU Poplar software divides convolutions and matrix products into the sum of several smaller matrix-vector products, equivalent to multiple calls to the AMP instruction, which allows for an efficient parallel GEMM implementation.
For each AMP call, the Colossus IPU’s AMP engines perform a parallel summation on blocks of 16 numbers, each block consisting of four sets of a 4-element FP16 dot product. The multiplicands in each dot product are aligned, compressed redundantly, then rounded with partial truncation to yield a result in IEEE FP32 format. Each of the four FP32 results, from each of the four dot products in a block, is summed sequentially according to IEEE FP32 addition. Finally, previously accumulated partial sums of products, in FP32 or FP16, can be fetched from memory, added to the block result, and stored back to memory. If the accumulated partial sums of products are FP16, these are first expanded to FP32, then added, then rounded back to FP16, then stored. This rounding mode can be either Round to Nearest (ties to even) or Stochastic Rounding, discussed below.
The IPU’s AMP operation supports different forms of mixed precision accumulation, with different precision of the input multiplicands and the partial sums of products (both loaded and output):
FP32.32: AMP operation with FP32 input multiplicands as well as FP32 partial sums of products, which achieves 16 MACs (32 FLOPs) per tile per cycle;
FP16.32: AMP operation with FP16 input multiplicands and FP32 partial sums of products, which achieves 32 MACs (64 FLOPs) per tile per cycle;
FP16.16: AMP operation with FP16 input multiplicands and FP16 partial sums of products, achieving 64 MACs (128 FLOPs) per tile per cycle.
AMP precision |
Multiplicands |
Loaded/stored partials |
MACs per cycle |
FLOPs per cycle |
|---|---|---|---|---|
FP32.32 |
FP32 |
FP32 |
16 |
32 |
FP16.32 |
FP16 |
FP32 |
32 |
64 |
FP16.16 |
FP16 |
FP16 |
64 |
128 |
As shown in Table 5.1, reducing the bit width of the accumulated partial sums of products is crucial to improving the hardware complexity and power consumption. It also leads to a better use of the available memory bandwidth, as demonstrated by the IPU’s AMP engine with FP16.16 precision, which delivers twice the throughput of its FP16.32 counterpart.
6. Mixed-precision training
Numerous works have studied the viability of low-precision number formats for training deep neural networks, gauging the accuracy achieved with reduced precision on different tasks. For the efficient training and inference of deep learning models, it is possible to combine the use of distinct numerical precision formats for different parts of the network using mixed precision, relying on FP16.16 or FP16.32 mixed precision accumulation for convolutions and matrix multiplications, and targeting other blocks, such as normalization and softmax layers, with higher precision arithmetic.
This can be combined with FP32 master weights, where a copy of the network parameters is kept in full precision throughput training. These parameters are converted to FP16 precision whenever they are used for computation. Although this solution maintains the FP32 network accuracy, it comes with the cost of duplicating the storage of weights and requires a down conversion each time the weights are used.
7. Deterministic versus stochastic rounding
Stochastic rounding, natively supported by the IPU, can be used with mixed precision training to help alleviate the precision loss when using FP16 partials (in 16.16 AMPs) or to enable training without an FP32 copy of the master weights. In contrast to deterministic rounding, which always outputs the same value for a given input, the decision about which output to produce in stochastic rounding is non-deterministic. For quantization of the input \(x\) with quantization step \(\mathrm{\Delta}\), the stochastic rounding probability equation is:
Where the probability of rounding carry into the result mantissa is proportional to the value of the integer formed by those intermediate bits, which were beyond the destination precision. In practice, this is achieved using uniformly distributed random bits, which are then added to the mantissa of the higher precision input, aligned to its least-significant bit up to the largest insignificant bit of the destination format. This sum is then truncated to the destination format.
Stochastic rounding has the nice property of producing an unbiased quantisation (where \(\mathbb{E}\left\{ Q_{s}\left( x \right) \right\} = x\)), despite adding a level of tolerable error. This means that, over many such additions, the added quantisation noise has zero mean, and the count of injected carries approximates what would have been propagated by accumulation at higher precision.
Stochastic rounding improves the precision of accumulations when many small-magnitude values contribute to forming a larger-magnitude result, such as for weight updates in neural network training. It commonly allows neural networks to train with exclusively FP16 weights, where otherwise FP32 master weights would be required.
To illustrate the performance effectiveness of stochastic rounding, Fig. 7.1 shows the test accuracy of ResNet50 trained on ImageNet for batch size 4 with SGD and different mixed-precision formats:
FP32: FP16.16 AMP and FP32 master weights
FP16RN: FP16.16 AMP and FP16 master weights without stochastic rounding
FP16SR: FP16.16 AMP and FP16 master weights with stochastic rounding
The results show that in this case the IEEE FP16 master weights with stochastic rounding can attain the IEEE FP32 state-of-the art accuracy.
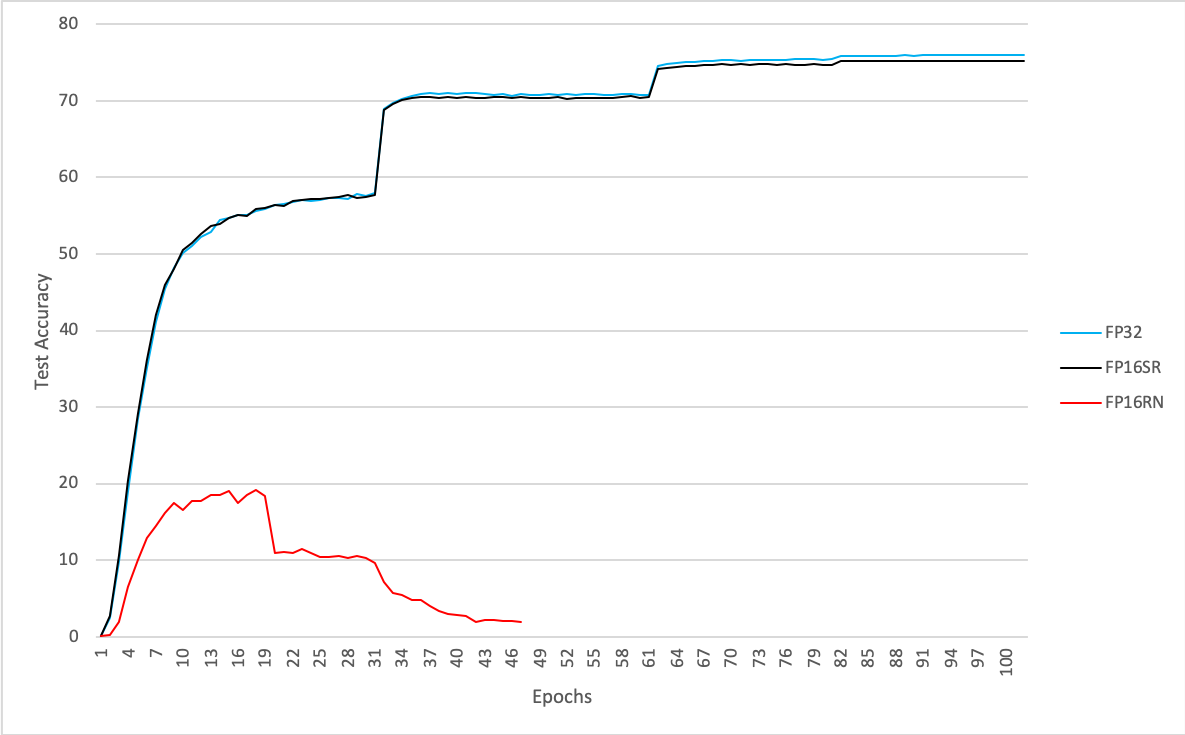
Fig. 7.1 Test accuracy with different mixed-precision formats
Fig. 7.2 shows the MLM+NSP training loss for BERT base with IEEE FP16 master weights, with and without stochastic rounding. As can be seen, without stochastic rounding the loss is degraded slightly from 1.64 to 1.77.
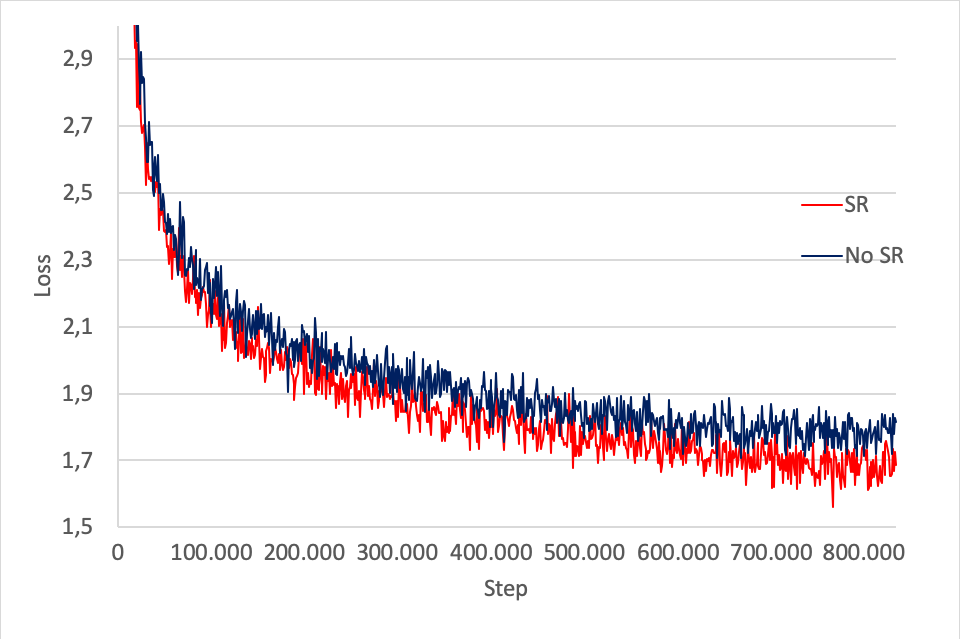
Fig. 7.2 BERT base training loss for FP16 master weights with and without stochastic rounding
8. Loss scaling
As mentioned before, reducing the representation word length for data comes with a reduction in the range of represented values, which is in turn limited by the use of a fixed exponent bias.
Naturally, different signals in the networks require different ranges of exponent which, for some quantities such as gradients, cannot be guaranteed to always be covered by the format used. To avoid formats that favour range over precision, through the use of unnecessarily large exponent fields such as bfloat16, the solution is to consider that the loss of the network can be scaled up. Due to the chain rule property of backpropagation, amplifying the loss efficiently propagates the scaling factor to all gradients in the network, and is equivalent to using a variable exponent bias without additional hardware support. The scaling factor can be easily accounted for during parameter update to ensure accurate results.
To simplify the application of low-precision numerical formats for the training of deep neural networks, automatic loss scaling can be used. By algorithmically scaling the loss before the backward pass, and compensating for this scaling during weight update, it can be guaranteed that the magnitude of the gradients is well adjusted for representation by the chosen floating-point format. When training different deep neural network models, the backoff algorithm can be used to dynamically control the scaling factor, based on increasing the loss scaling factor until a numerical overflow occurs, in which case the scaling factor is reduced by a factor of 2.
9. Summary
In summary, mixed precision has become the standard arithmetic for accelerating deep learning models, as it allows better power efficiency due to improved compute and data transfer throughputs. Deep learning models, commonly trained with IEEE single-precision formats, are seen to be robust to the reduction in representation length when using mixed precision as they can match state-of-the performance.
The use of IEEE 16- and 32-bit floating point formats in the Colossus IPU and Poplar software provides the user with the means to seamlessly port their models to the IPU and to readily use mixed precision. At the software level, it is possible to choose the precision of the GEMM partial accumulation in the model by selecting the FP16.16 or the FP16.32 mixed precision variant. In addition, the user can enable the IPU’s stochastic rounding, which removes the need for FP32 master weights. When combined with FP16.16 AMP, FP16 master weights with stochastic rounding gives the opportunity of delivering reduced memory overhead without compromising the FP32 state-of-the art accuracy.
Finally, in order to prevent the underflow of gradient values, the user can fix the value of their loss scaling or opt for the automatic loss scaling approach, which will algorithmically determine the best value of scaling to be applied.