2. Programming with Poplar

You can use Poplar library functions to define graph operations and control the execution and profiling of code on the IPU.

Code can be compiled to run on IPU hardware, a simulated IPU Model or the host CPU. Running on an IPU Model or the CPU may be useful for functional testing of simple code when you do not have access to IPU hardware.

The IPU Model is a simulation of the behaviour of the IPU hardware. It does not completely implement every aspect of a real IPU. For example:

• The IPU Model does not fully support replicated graphs (see Section 2.4, Replicated graphs).

• The arithmetic results may differ from what would be obtained by using the IPU hardware.

• Random number generation in the IPU Model is not the same as the hardware. In particular, every simulated tile has the same hard-coded seed (the setSeed() function is a no op). This means all IPU Model codelets will produce the same results every time they are run. Therefore, the IPU Model should not be used to verify any training or accuracy if the graph includes any random number generation.

If you encounter an out of memory error, it may be useful to run on the IPU Model device to debug the problem.

Consider the situation in which the event trace is being used to investigate a graph that creates a tile memory imbalance. In this case, running on the IPU will lead to an out of memory exception before the report is generated. Running on the IPU Model instead of actual hardware will still run out of memory, but the code will run to completion so the report can be generated.

Code running on a CPU device will be faster than the IPU Model, because it does not have the overhead of modelling the IPU hardware. CPU code runs with a single worker thread as if on a single tile on a single IPU. This means you do not need to think about tile allocation or the limited tile memory when initially developing vertex code. Running on a CPU device may also be useful for unit testing of vertices.

Interrogating a CPU device by calling Engine functions such as getBytesPerTile() or getTileClockFrequency() may not return accurate or meaningful results.

If you want to profile your code, you will need to run on either IPU hardware or the IPU Model.

2.1. Poplar programming model

For a more detailed introduction to the IPU architecture and programming model, see the IPU Programmer’s Guide.

A Poplar computation graph defines the input/output relationship between variables and operations. Each variable is a multi-dimensional tensor of typed values and can be distributed across multiple tiles.

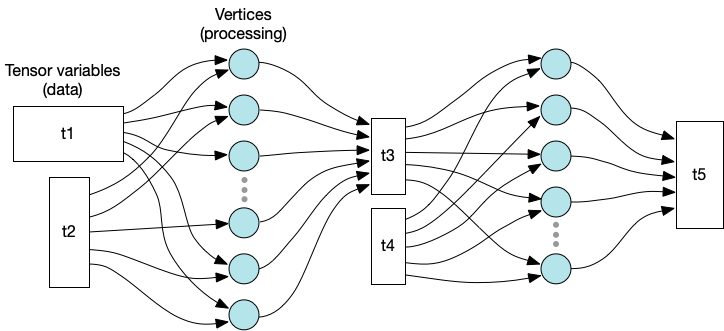
Fig. 2.1 Graph representation of variables and processing

The vertices of the graph are the code executed in parallel by the tiles. Each tile executes a sequence of steps, which form a compute set containing one or more vertices.

The edges of the graph define the data that is read and written by the vertices. Each tile only has direct access to the tensor elements that are stored locally.

Each vertex always reads and writes the same tensor elements. In other words, the connections defined by the execution graph are static and cannot be changed at run time. However, the host program can calculate the mapping and graph connectivity at run time when it constructs the execution graph. See Poplar tutorial 6 in the Graphcore GitHub repository for an example.

The placement of vertices and tensor elements onto tiles is known as the tile mapping.

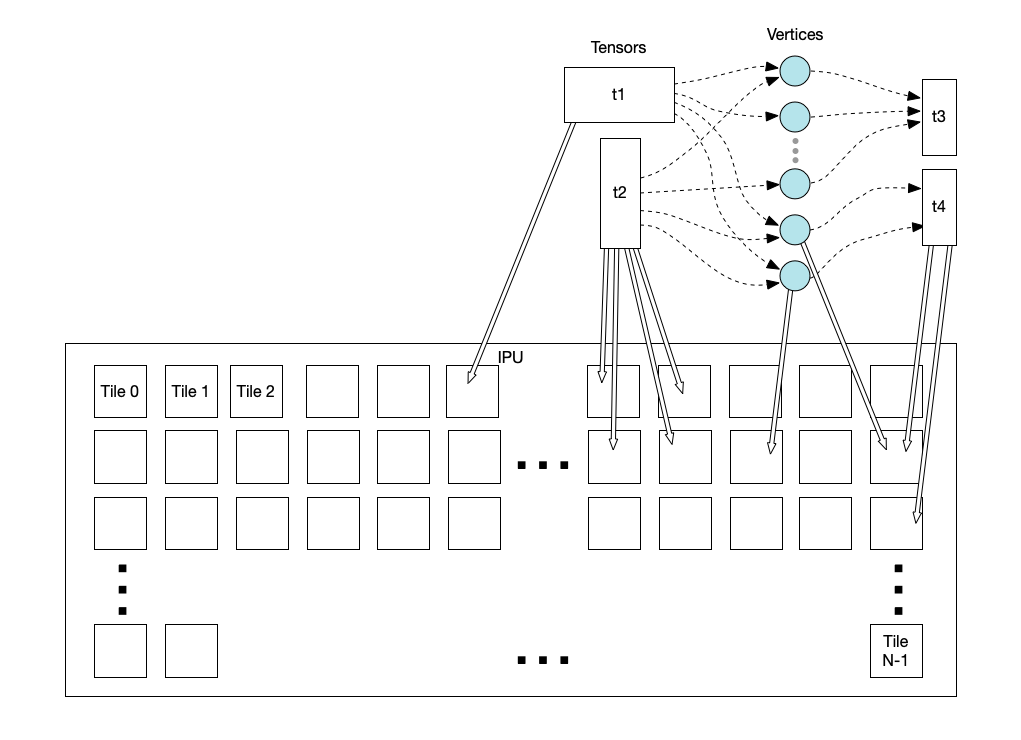
Fig. 2.2 Mapping tensors and vertices to tiles

2.2. The structure of a Poplar program

A Poplar program performs the following tasks:

• Find or create the target device type as a Device representing physical IPU hardware or a simulated IPUModel.

• Create a Graph object which will define the connections between computation operations and data, and how they are mapped onto the IPUs.

• Create one or more Program objects which will control the execution of the graph operations.

• Define the computations to be performed and add them to the Graph and Program objects. You can use the functions defined in Poplar and PopLibs, or you can write your own device code.

• Create an Engine object, which represents a session on the target device, using the Graph and Program objects.

• Connect input and output streams to the Engine object, to allow data to be transferred to and from the host.

• Execute the computation with the Engine object. This will compile your graph code and load it onto the IPU, along with any library functions required, and start execution.

The Poplar and PopLibs libraries also include programs for a wide range of operations on tensor data.

For more detailed descriptions and examples of each of these steps, see the tutorials in the Graphcore GitHub tutorials.

2.2.1. Program flow control

A program object can be constructed by combining other program objects in various ways. There are several sub-classes of Program that provide flow control.

The simplest of these is Sequence, which executes a number of sub-programs sequentially. There are also Program classes for executing loops, and for conditional execution.

Looping

Looping is supported by the Repeat* classes and the PopLibs counted loop functions, which provide a more flexible interface.

There are two types of repeat programs:

• Counted: this iterates a fixed number of times (a compile-time constant)

• While: there are two repeat programs (RepeatWhileTrue and RepeatWhileFalse) which will iterate while the condition is met. Any non-zero value of the predicate is treated as true.

The counted repeat program iterates a fixed number of times. PopLibs provides a more flexible interface with the loop functions in the popops library.

Each of the functions in popops/Loop.hpp returns a program object that implements a “for” loop. There are several versions of these functions that provide varying amounts of control over the loop variables; for example specifying the start, step and end values of the loop counter. The number of iterations can be defined at run time.

The loop count variable can be made available to the program in the body of the loop (unlike loops created with Repeat).

A basic outline for creating a countedForLoop() is shown below:

count = graph.addVariable(poplar::UNSIGNED_INT, {1});
limit = graph.addVariable(poplar::UNSIGNED_INT, {1});
loopBodyProg = Sequence();
popops::mapInPlace(graph, Add(_1, _2), {bodyVar,count}, loopBodyProg,
                    "/bodyFunction");
prog.add(poputil::countedForLoop(graph, count, 0, limit, 1, loopBodyProg,
                                    "/countedForLoop"));

Conditional execution

The If program is equivalent to an if-then-else: it runs one of two programs depending on the value of a scalar tensor. Any non-zero value of the predicate is treated as true. You can use an empty Sequence for the “else” branch if you just want a simple “if” conditional.

The Switch program runs one of a number of programs depending on the value of a tensor. You can also define a default case for when the value of the tensor does not match one of the switch values.

2.2.2. What happens at run time

When you run your program on the host, the Poplar run-time will compile your graph to create object code for each tile. The code may come from Poplar or PopLibs library functions, or from vertex code you write yourself (see Section 2.7, Device code), and will be linked with any required libraries.

This object will contain:

1. The control-program code from your graph

2. Code to manage exchange sequences

3. Initialised vertex data

4. The tensor data mapped to that tile

The host program will load the object code onto the target device, which is then ready to execute the program.

2.3. Virtual graphs

A graph is created for a target device with a specific number of tiles. It is possible to create a new graph from that, which is a virtual graph for a subset of the tiles. This is effectively a new view onto the parent graph for a virtual target, which has a subset of the real target’s tiles and can be treated like a new graph. You can add vertices and tensors to the virtual sub-graphs. These will also appear in the parent graph.

Any change made to the parent graph, such as adding variables or vertices, may also affect the virtual sub-graph. For example, a variable added to the parent graph will appear in the sub-graph if it is mapped to tiles that are within the subset of tiles in the virtual target.

Virtual graphs can be used to manage the assignment of operations to a subset of the available tiles. This can be used, for example, to implement a pipeline of operations by creating a virtual graph for each stage of the pipeline and adding the operations to be performed on those tiles.

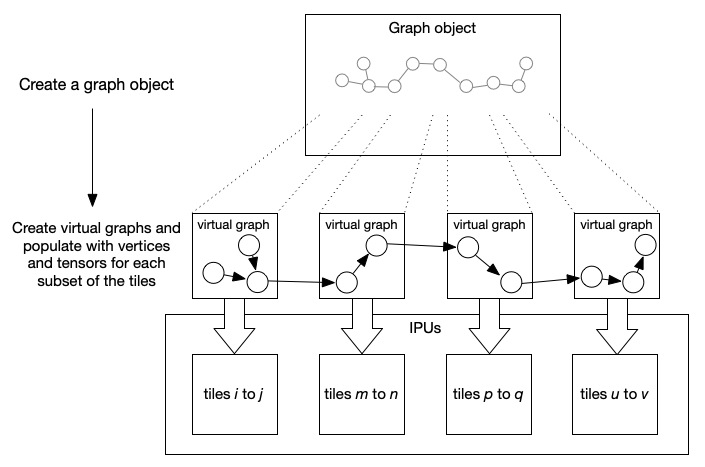
Fig. 2.3 Mapping a pipeline of operations to tiles using virtual graphs

There are several versions of the createVirtualGraph function, which provide different ways of selecting the subset of tiles to include in the virtual target.

2.4. Replicated graphs

You can also create a replicated graph. This effectively creates a number of identical copies, or replicas, of the same graph. Each replica targets a different subset of the available tiles (all subsets are the same size). This may be useful, for example, where the target consists of multiple IPUs and you want to create a replica to run on each IPU (or group of IPUs) in parallel.

Any change made to the replicated graph, such as adding variables or vertices, will affect all the replicas. A variable mapped to tile 0, for example, will have an instance on tile 0 in each of the replicas.

Creating a replicated graph can be done by passing a replication factor to the Graph constructor (see Section 2.4.1, Creating a replicated graph).

Note: Replicated graphs are not supported when running on an IPU Model.

As an example, imagine you have a graph which targets two IPUs. You can run four copies of it, in parallel, on eight of the IPUs in your system by creating the two-IPU graph and replicating it four times. This can be done using either of the techniques above, each of which has advantages and disadvantages, summarised in the following descriptions.

2.4.1. Creating a replicated graph

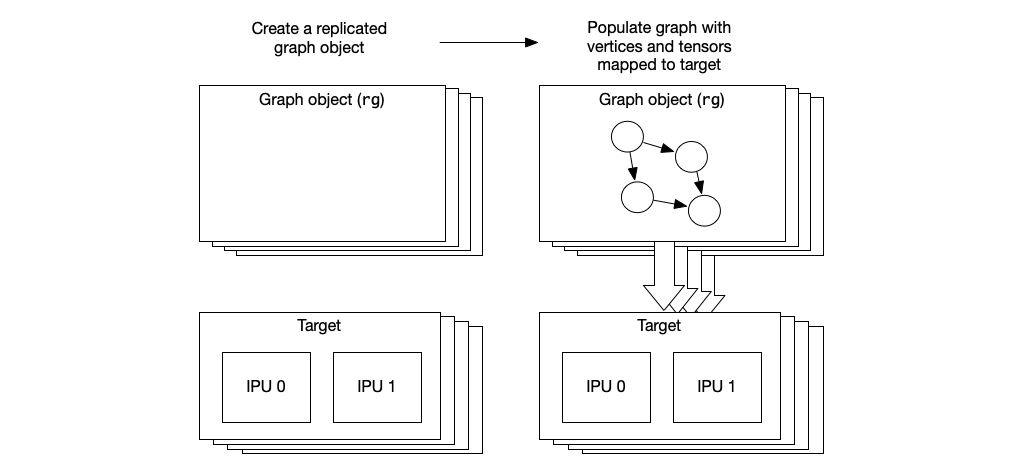
Fig. 2.4 Creating a replicated graph

We start by creating a replicated graph using the graph constructor:

// Create a graph with 4 replicas for each 2 IPUs
Graph rg = Graph(target, replication_factor(4));

We can add variables and vertices to this graph as usual. These additions will be applied to every replica. This graph only exists as a replica, with no parent graph that can be used to make modifications differently to each replica. Therefore, as all the replicas are guaranteed to be identical, the graph only needs to be compiled once. Copies of the object code are then loaded onto each of the pairs of IPUs when the program runs. Each instance of the replica is given a unique ID at load time; this can be used to identify it in functions such as crossReplicaCopy.

Any functions that rely on the existence of a parent, such as getTopLevelGraph, will fail.

2.5. Data streams and remote buffers

Memory external to the IPU can be accessed in two ways. Data streams enable the IPU to transfer data to and from host memory. Remote buffers enable the IPU to store data in external (off-chip) memory.

2.5.1. Data streams

Data streams are used for communication between the host and the IPU device. The data transfers are controlled by the IPU.

Each stream is a unidirectional communication from the host to the device, or from the device to the host. A stream is defined to transfer a specific number of elements of a given type. This means the buffer storage required by the stream is known (the size of the data elements times the number of elements).

The Poplar graph compiler will merge multiple stream transfers into a single transfer (up to the limits described in stream_buffer_size_limit).

Device-side streams

A stream object, represented by the DataStream class, is created and added to a graph using the addHostToDeviceFIFO() or addDeviceToHostFIFO() functions. The stream is defined to have:

• A name for the stream

• The type of data to be transferred

• The number of elements to be transferred

A host-to-device stream can also have a replication mode, if it is connected to a replicated graph. This defines whether a single stream will send the same data to all the replicated graphs (broadcast mode) or there will be a stream per replica.

Stream data transfer is done with a Copy program which copies data from the stream to a tensor, or from a tensor to the stream.

Host-side stream access

On the host side, a data stream is connected to a buffer allocated in memory. You connect a buffer to the stream using the connectStream() function of an Engine object. This can, optionally, be implemented as a circular buffer to support more flexible transfers.

In order to synchronise with the data transfers from the IPU, a callback is connected to the stream using the connectStreamToCallback() function. Callback implementations are derived from the StreamCallback interface and have a pointer to the stream buffer as an argument.

• For a device-to-host transfer, the callback function will be called when the transfer is complete so that the host can read the data from the buffer.

• For a host-to-device stream, by default the callback function will be called immediately before the IPU transfers the buffer contents to device memory. The host-side code should populate the stream buffer and then return.

Stream buffer size limit

The IPU has a memory address translation table which defines the external memory address range it can access. As a result, there is a maximum buffer size for data transferred by a stream. This limit is 256 MB per stream copy operation for Mk2. More data can be transferred by a sequence of copies, separated by sync operations, so that the buffer memory can be reused for each transfer.

To support stream copies that may exceed the buffer capacity, Poplar will split larger stream copies into a sequence of stream copies with distinct sync IDs. The size at which a stream copy is split is determined by splitLimit option. You can specify this when creating the data stream with addHostToDeviceFIFO() and addDeviceToHostFIFO(). This limit is smaller than the maximum stream copy transfer limit to account for internal Poplar streams which are added.

Each IPU has its own translation table. So, if there are multiple IPUs, this limit applies to each IPU individually.

2.5.2. Optimising host data transfers

There are several things you can do to optimise the use of data streams to and from the host. These are described below.

Prefetch

You can specify that the the IPU should call the callback function as early as possible (for example, immediately after it releases the stream buffer from a previous transfer). The host is then able to fill the buffer in advance of the transfer, meaning the IPU spends less time waiting for the host.

This mode of operation is known as prefetch. It is only available for host-to-IPU stream copies and requires that the stream’s data buffer never overlaps with other streams (overlap may take place if any of the copy programs using the stream optimize memory consumption).

The callback function returns a value that indicates if the buffer was filled.

If there is data available to fill the buffer, the callback function should return Result::Success. The next time a transfer takes place, it skips the fetch() function call and only performs a call to complete().

Otherwise, if data is not available (either because it is the end of the stream, or the data is not ready yet), then the callback returns Result::NotAvailable.

Note

The Engine option exchange.streamBufferOverlap may be used to modify overlap strategy.

This can be useful in some circumstances, for example, if you want to be certain that prefetch will be used but the default overlap strategy is preventing this.

• any (default): Poplar is free to overlap streams providing there is no clash between them.

• hostRearrangeOnly: Poplar will only overlap streams with rearrangeOnHost property set.

• none: Poplar will never overlap streams, regardless of the absence of collisions.

Multibuffering

Data streams also supports multibuffering. Multibuffering means that a single data stream uses many buffers, instead of one. Having many buffers allows better I/O performance by getting the IPU and the host to work concurently, on different buffers. The number of buffers used by a stream is called its depth. Fig. 2.5 shows how multibuffering using a buffering depth of 2 improves IPU to host communication:

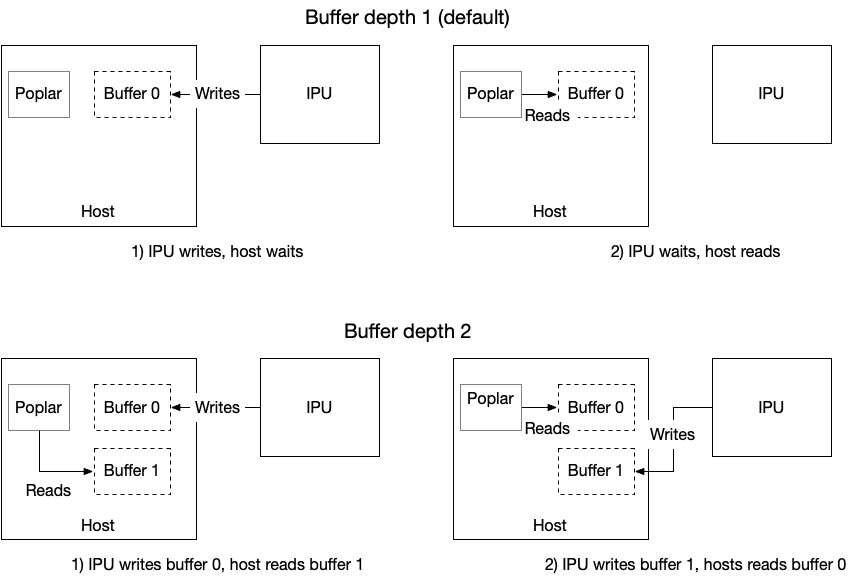
Fig. 2.5 Host and IPU communication with and without multibuffering

You can enable multibuffering for a data stream by setting its depth using the option bufferingDepth in the OptionFlags passed to the addHostToDeviceFIFO() or addDeviceToHostFIFO() functions.

2.5.3. Remote memory buffers

The IPU can also access off-chip Streaming Memory as a remote buffer. This may be host memory or external memory associated with the IPU system. This is not used for transferring data to the host, but just for data storage by the IPU program. Accesses to and from the remote buffer are much faster than data streams because they are entirely driven by the IPU during program execution and do not need to interact with the host.

A RemoteBuffer object is created and added to the graph with the addRemoteBuffer() function of the graph object. Data transfers to and from the remote buffer are performed using a Copy program; this copies data from the buffer to a tensor, or from a tensor to the buffer.

The data type and size of the remote buffer are defined when it is created. The definition of the buffer and the parameters to the Copy program allow for very flexible addressing.

You can think of the remote buffer containing a number of “rows” of data to be transferred. (These rows do not need to correspond to the structure the tensor being transferred or the organisation of the data in the buffer, but are just a way of managing data transfers.)

The size of each row and the number of rows are parameters to addRemoteBuffer() when the buffer is created:

• numElements is the number of data items in each row

• repeats is the number of rows in the buffer

Each Copy program can copy one or more rows of data to or from the remote buffer The rows to be copied are specified by the offset parameter to the Copy program. The number of offsets specifies the number of rows to copy. This cannot be larger than repeats. However, each row is implemented as a separate transfer.

Remote buffer restrictions

• All copies to and from a given RemoteBuffer must be from the same IPU (each remote buffer is associated with exactly one IPU)

• The size of a single transfer can not exceed 256 MB. In other words, each row must be less than 256 MB. The size of the remote buffer can be larger than 256 MB, depending on the value of the repeats parameter.

• On IPU-Machines like the IPU-M2000 or the Bow-2000, and Pod systems, each IPU may use up to one quarter of the Streaming Memory of the IPU-Machine. However, each IPU reserves 256 MB from this for data streams. For example, with 32 GB attached to an IPU-M2000, each of the four IPUs have (8 GB - 256 MB) available to be used for remote buffers.

• By default IPUs are limited to (16 GB - 256 MB) of remote buffers each, regardless of the size of the Streaming Memory. If using more than 16 GB per IPU, the engine option target.extendedMemory must be set to “true”. This has a slight performance impact for copies so is disabled by default.

2.6. IPU-Link and sync configuration

Multiple IPUs can be connected with IPU-Links to share data. There are also synchronisation (sync) signals that are used to indicate when IPUs are ready to exchange data and that data exchange is complete. These sync signals are also used to synchronise host transfers and access to remote buffers.

2.6.1. Link topologies

There are two ways of connecting IPU-Links and sync signals: in a mesh or as a torus. The mesh structure is similar to a ladder, where pairs of IPUs form each rung. In a torus, the ends of the “ladder” loop round to form a closed loop.

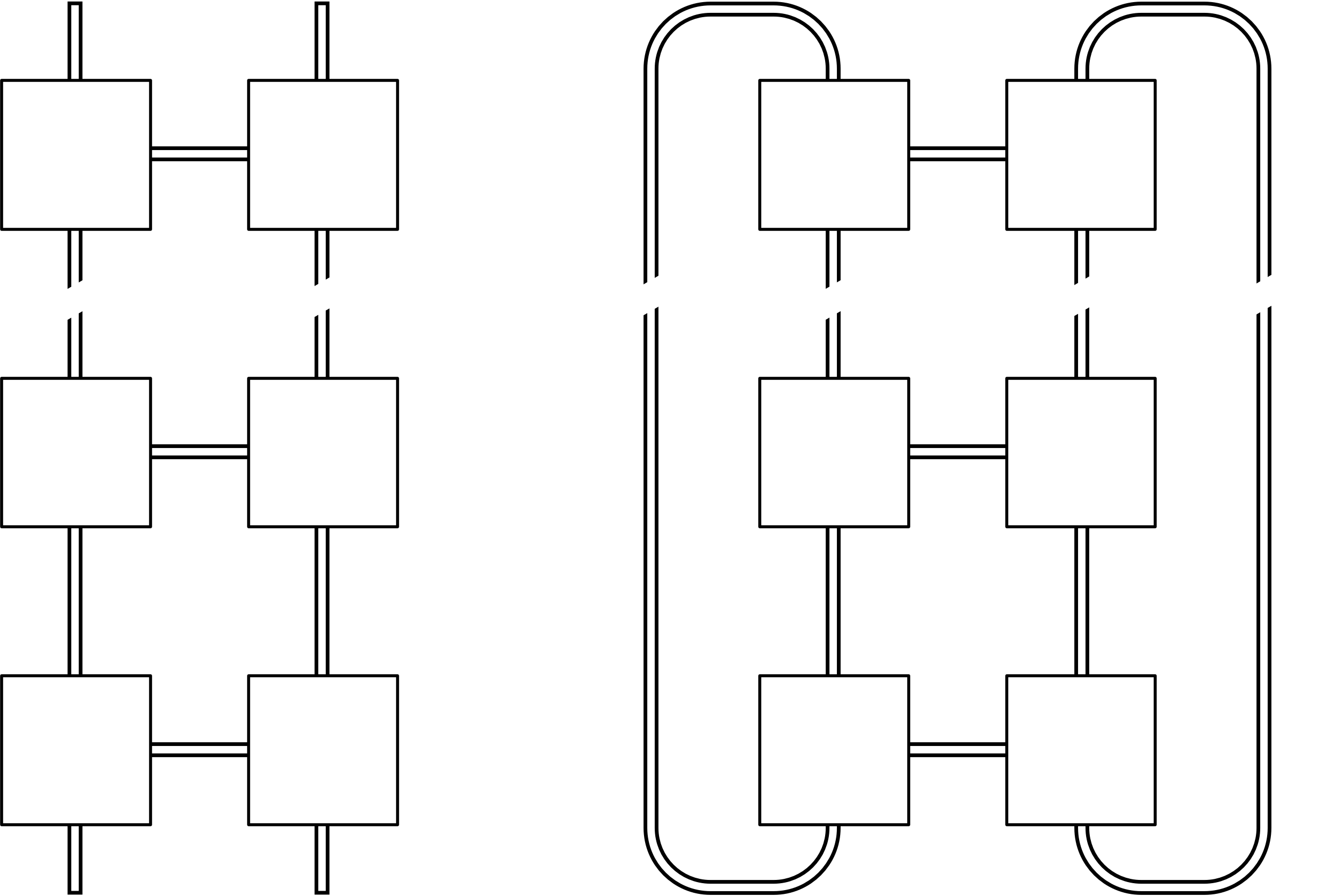
Fig. 2.6 Mesh and torus link topologies

When a target device is created in a Poplar program, the topology is defined by the ipuLinkTopology option to the Target object.

2.6.2. Sync groups

Each IPU can be allocated to one or more “sync groups”. At a synchronization point, all the IPUs in a sync group will wait until all the other IPUs in the group are ready.

Sync groups can be used to allow subsets of IPUs to overlap their operations. For example, one sync group can be performing data transfers to or from the host, while another group is processing a previous batch of data.

There are four sync groups on the Mk2 IPU: GS1, GS2, GS3 and GS4. Only the first two sync groups, GS1 and GS2, can be used for syncing with the host. The Engine option target.syncReplicasIndependently controls whether to use GS1 or GS2 for host sync; if the value is true it uses GS1, if false it uses GS2.

You can configure the sync groups as appropriate for your application. The allocation of IPUs to the sync groups (GS1 and GS2) is configured using the syncConfiguration option when creating a target. All the configurations have names of the form “<GS1>And<GS2>”, where “<GS1>” and “<GS2>” are strings representing which subsets of IPUs are in that sync group:

• intraReplica: syncs all the IPUs inside each replica; IPUs do not sync across replica boundaries

• ipu: syncs each IPU individually

• All: syncs all the IPUs, even across instances and ILDs

• Ladder: syncs all even numbered IPUs together and, separately, all odd numbered IPUs together

You can set the syncConfiguration in the following way:

poplar::OptionFlags options;
options.set("syncConfiguration", "intraReplicaAndLadder");
poplar::DeviceManager manager = poplar::DeviceManager::createDeviceManager();
manager.getDevices(poplar::TargetType::IPU, N, options)

The options are:

• intraReplicaAndAll (default):

  • GS1 (intraReplica) is used for synchronisation between the IPUs in each replica of a replicated graph (or all IPUs if there is no replication).

  • GS2 (All) is used for synchronisation between all IPUs.

• ipuAndAll:

  • GS1 (ipu) is used for synchronisation of each IPU individually.

  • GS2 (All) is used for synchronisation between all IPUs.

• intraReplicaAndLadder:

  • GS1 (intraReplica) is used for synchronisation between the IPUs in each replica of a replicated graph (or all IPUs if there is no replication).

  • GS2 (Ladder) is used by two independent subsets of IPUs. All the odd-numbered IPUs are synchronised with the other odd IPUs, and similarly all the even-numbered IPUs are synchronised with the other even IPUs. These two subsets can then execute independently of one another, so that they can alternate between one set doing host I/O, for example, while the other is computing.

Please note that the configuration intraReplicaAndLadder can only be used when the number of IPUs per replica is 2 or more. Additionally, note that all the sync groups are configured statically before the execution of the program and cannot be changed over the lifetime of the program. Consider a concrete example, represented here, where we have 2 IPUs per replica, and the replication factor is 2; each square represents an IPU, and the number within is the IPU ID:

 +---+    +---+
 | 0 | -- | 2 |
 +---+    +---+
   |        |
 +---+    +---+
 | 1 | -- | 3 |
 +---+    +---+

 \___/    \___/
replica  replica
   0        1

In this example, we would have the following sync grouping (the numbers are the IPU IDs):

• intraReplica: {0, 1}, {2, 3}

• All: {0, 1, 2, 3}

• ipu: {0}, {1}, {2}, {3}

• Ladder: {0, 2}, {1, 3}

The bracketed numbers show the subsets of IPUs (for example, those in a replica) that are able to sync independently of one another. These subsets can be individual IPUs, the IPUs in a replica, or all the IPUs. The subsets can be in ether sync group GS1 or GS2.

The syncConfiguration options are summarised in Table 2.1. Note that target.syncReplicasIndependently just changes which sync group is used for host communication.

Table 2.1 Use of sync groups by Poplar

syncConfiguration	Sync group	target.syncReplicasIndependently
		false (default)	true
intraReplicaAndAll (default)	GS1	Communication between IPUs within each replica (or all IPUs if the graph is not replicated). Remote buffer access.	Communication between IPUs within each replica (or all IPUs if the graph is not replicated). Remote buffer access. Host communication.
	GS2	Communication between replicas (all IPUs). Host communication.	Communication between replicas (all IPUs).
ipuAndAll	GS1	Remote buffer access.	Remote buffer access. Host communication.
	GS2	Communication between all IPUs. Host communication.	Communication between all IPUs.
intraReplicaAndLadder	GS1	Communication between IPUs within each replica (or all IPUs if the graph is not replicated). Remote buffer access.	Communication between IPUs within each replica (or all IPUs if the graph is not replicated). Remote buffer access. Host communication.
	GS2	Communication between all IPUs with even IDs, and between all IPUs with odd IDs. Host communication.	Communication between all IPUs with even IDs, and between all IPUs with odd IDs.

2.7. Device code

Each vertex of the graph is associated with some device code. This can come from a standard program object or library function, or you can write your own as a codelet. Codelets are specified as a class that inherits from the poplar::Vertex type. See Section 3, Understanding vertices for more information.

You can add a codelet to your graph by using the Graph::addCodelets function. This will load the source file and compile the codelet when the host program runs. See the adder example provided with the Poplar distribution.

You can also pass compilation options (for example “-O3”). The code is compiled for both the host and for the IPU so the program can be run on IPU hardware or on the host.

There are a couple of predefined macros that may be useful when writing vertex code. __POPC__ is defined when code is compiled by the codelet compiler. The macro __IPU__ is defined when code is being compiled for the IPU (rather than the host).

Graphcore’s tutorials include an introductory tutorial on creating codelets and compute sets with Poplar.

You can also write codelets in assembly language for the IPU. See Section 10, Writing vertices in assembly for more information.

2.7.1. Pre-compiling codelets

There is a command line tool to pre-compile codelets. This reduces loading time, and allows you to check for errors before running the host program.

The codelet compiler, popc, takes your source code as input and creates a graph program object file (conventionally, with a .gp file extension). For example:

$ popc codelets.cpp -o codelets.gp

This object file can be added to your graph in the same way as source codelets, using the same Graph::addCodelets function. See the adder_popc example provided with the Poplar distribution.

The general form of the popc command is:

$ popc [options] <input file> -o <output file>

The command takes several command line options. Most are similar to any other C compiler. For example:

-D<macro>	Add a macro definition
-I<path>	Add a directory to the include search path
-g	Enable debugging
-On	Set the optimization level (n = 0 to 3)

For a full list of options, use the --help option.