3. Concepts

The building blocks of PopXL are the intermediate representation (IR), graphs, tensors and ops. This section describes these concepts. Further information on how each concept applies to PopXL can be found in the referenced sections.

3.1. IRs

An IR is the intermediate representation in PopXL of an executable program that can be run using a PopXL session. A Python process can initialise multiple IRs.

An IR contains one main graph (Section 9.1, Main graph), created on IR initialisation, and multiple graphs (Section 9.2, Graphs) that you create. The main components of an IR are shown in Fig. 3.1.

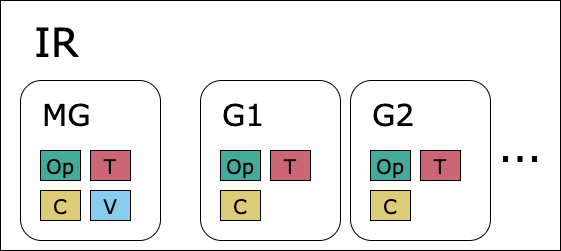
_images/popxl_building_blocks.png

Fig. 3.1 An IR contains a main graph (MG) and multiple other graphs (G). Graphs can contain ops, intermediate tensors (T) and constant tensors (C). The main graph can also contain intermediate, constant and variable tensors (V).

3.2. Graphs

A graph in the IR (Section 9, Graphs) is a computational graph: a network of operations (ops) and tensors. There are two types of PopXL graphs: the main graph (Section 9.1, Main graph) and graphs (Section 9.2, Graphs). An example is shown in Fig. 3.2.

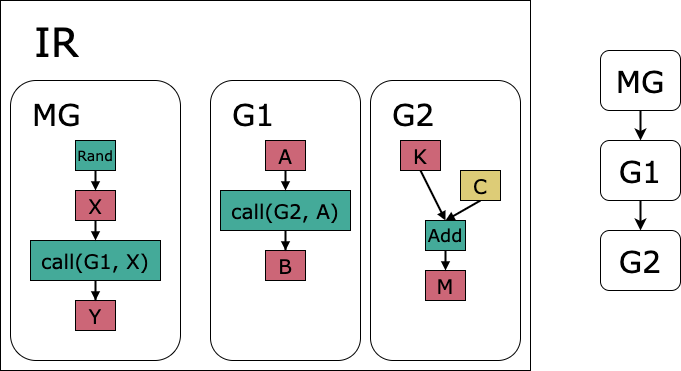
_images/popxl_calling_a_graph.png

Fig. 3.2 The main graph (MG) calls graph 1 (G1) which in turn calls graph 2 (G2). This creates a call tree which is depicted on the right. Op nodes are green, intermediate tensors are red and constant tensors are yellow.

  • The main graph (Section 9.1, Main graph) is the entry point of the IR (like the main() function in many programming languages). There is only one main graph per IR. The main graph can contain intermediate, constant and variable tensors.

  • Graphs (Section 9.2, Graphs) can be called by other graphs using the call or repeat op. If a graph has multiple call sites, the graph is outlined during lowering, leading to code reuse and reduced memory usage. A graph can only contain intermediate or constant tensors and not variable tensors. A graphs inputs and outputs are specified on graph creation.

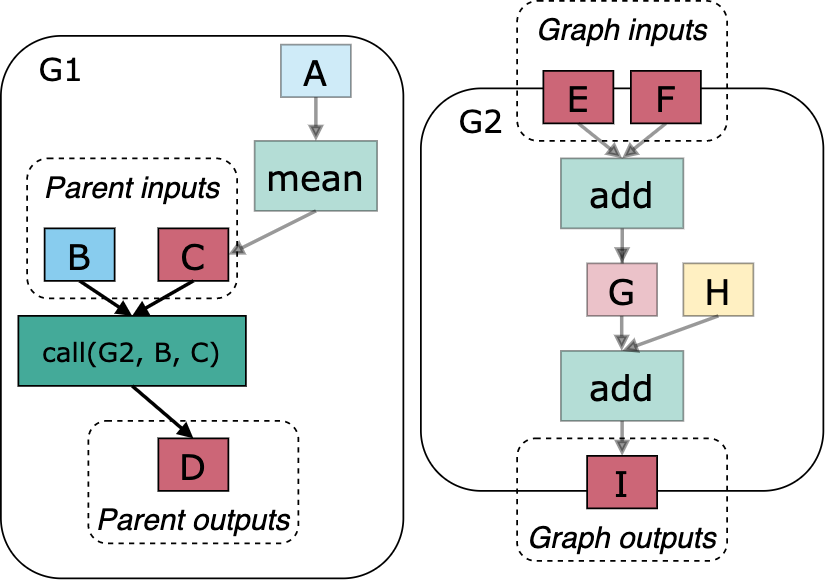
_images/popart_ir_graph_tensors.png

Fig. 3.3 Graph 1 (G1) calls graph 2 (G2) and passes the input tensors B and C - these are known as parent graph inputs. The call site creates a tensor D known as the parent graph output. Tensor B and C in G1 are mapped to tensors E and F, known as the graph inputs, in G2 at the call site. Similarly tensor I in G2, known as the graph outputs, are mapped to tensor D in G1.

When a graph is called, using the call or repeat op, the inputs must be provided by the calling graph, these tensors are known as parent inputs. Similarly tensors that are outputs at the call site are known as parent outputs. The parent inputs and outputs are specific to a call site. The input data can be either passed by reference or value, and this is determined by the user at the call site.

  • Subgraphs (Section 9.2, Graphs) have input and output tensors. Subgraphs can be called by other graphs using the call() or repeat() op. If a subgraph has multiple call sites, the subgraph is outlined during lowering, leading to code reuse and reduced memory usage. A subgraph can only contain intermediate or constant tensors and not variable tensors. Subgraphs have intermediate tensors which are marked as inputs or outputs. When a subgraph is called, the inputs must be provided by the calling graph. The input data can be either passed by reference or value, and this is determined by the user at the call site.

3.3. Tensors

Tensors (Section 6, Tensors) have a shape and data type, and sometimes initialisation data. A tensor is produced by a producer op and can have multiple consumer ops. There are three types of tensors: intermediate, variable and constant. Variable and constant tensors are initialised with data, while intermediate tensors are not.

  • Constant tensors contain data that cannot change.

  • Variable tensors contain data that is always live and hence the memory allocated to them is never freed. Typically model weights are kept on the IPU between runs and are therefore defined as variable tensors. Variable tensors are analogous to “global variables” in other programming languages, which can be accessed throughout the lifetime of the program.

  • Intermediate tensors are not initialised with data and are live from the time they are produced until their final consumer. Intermediate tensors are analogous to “local variables” in other programming languages, which are created and discarded dynamically as the program executes.

3.4. Operations

An operation or op (Section 7, Supported operations) represents an operation in the computational graph and can have input and output tensors.