10. Transforms

After an IR is built, you can use transforms or patterns to manipulate its graphs in a non-trivial way. Transforms are used to change a graph at the graph level, while patterns are usually used to change a specific operation repeatedly in a graph.

Currently, we support the following transforms:

  • Autodiff

10.1. Autodiff

In PopXL you can use autodiff() to perform automatic differentiation on a per-graph basis. This transform creates a graph (the gradient graph) to compute the gradients of a forward graph. It is declared as:

autodiff(graph: Graph,
          grads_provided: Optional[Iterable[Tensor]] = None,
          grads_required: Optional[Iterable[Tensor]] = None,
          called_graphs_grad_info: Optional[Mapping[Graph, GradGraphInfo]] = None,
          return_all_grad_graphs: bool = False)

The inputs are as follows:

  • graph is a forward graph.

  • grads_provided indicates for which outputs of graph we have gradients available for autodiff to use. For instance, if graph outputs both loss and accuracy, you might not want to provide gradients for accuracy. The default is that gradients are provided for all of the outputs of the forward graph.

  • grads_required indicates which inputs of the forward graph you want autodiff to calculate gradients for. The default is that gradients are required for all of the inputs to the forward graph.

  • called_graphs_grad_info and return_all_grad_graphs can be used to reduce computation of gradients when there are subgraphs that are called by multiple parent graphs.

    • return_all_grad_graphs indicates whether to return the gradient graphs for all the graphs that autodiff has been recursively applied to or just for the given graph. autodiff returns an GradGraphInfo object that includes the computational graph for computing the gradients if return_all_grad_graphs is set to False. It will return all the gradient graphs if return_all_grad_graphs is set to True.

      • You only need return_all_grad_graphs if and only if:

        • the graph you are applying autodiff to has calls to other subgraphs and

        • you need the gradients for those called subgraphs. This typically only happens when you want to apply autodiff to another graph that also calls these same subgraphs.

        For example, for graphs A, B and C, where:

        • A calls C

        • B calls C

        If you apply autodiff to B first and if you do not specify return_all_grad_graph, then you only get the gradient graph information for B, and not for C. If you specify return_all_grad_graphs, then you will get the gradient graph information for both B and C. Then, if you want to apply autodiff to A, which also calls C, you can reuse this gradient graph information for C. This means that autodiff will not have to create another gradient graph for C.

    • You use called_graphs_grad_info to provide the information for gradient graphs, which you have already calculated, as inputs to subsequent autodiff calls where that gradient graph information is needed.

The GradGraphInfo object contains all the information and tools you need to get a gradient graph:

  • graph: the associated gradient graph as produced by autodiff

  • forward_graph: the forward graph that autodiff was applied to

  • expected_inputs: the tensors from forward_graph that are required as inputs to the gradient graph.

  • expected_outputs: the tensors from the forward graph that have gradients as outputs of the gradient graph.

  • inputs_dict(fwd_call_info): the inputs to call the gradient graph.

  • fwd_graph_ins_to_grad_parent_outs(grad_call_info): the mapping between forward subgraph tensors and gradient call site tensors. Note that grad_call_info is the call site information of the gradient gradient graph (Fig. 10.1).

  • fwd_parent_ins_to_grad_parent_outs(fwd_call_info, grad_call_info): the mapping between forward call site inputs and gradient call site outputs. It can be used to get the gradient with respect to a specific input (Fig. 10.1).

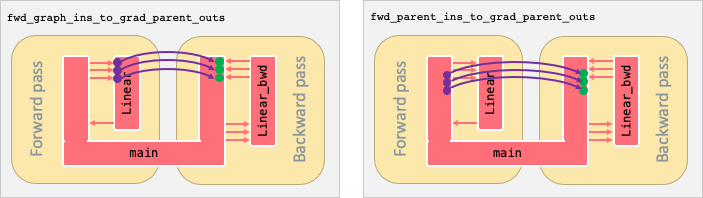
_images/autodiff_fwd_graph_ins_vs_fwd_parent_ins.png

Fig. 10.1 The difference between the mappings returned by fwd_graph_ins_to_grad_parent_outs (left) and fwd_parent_ins_to_grad_parent_outs (right) for an example graph Linear.

You can then use the information for the gradient graph returned by autodiff to get the required gradients. The partial derivatives of the loss with respect to the graph outputs of the forward graph are the first inputs of the gradient graph. Listing 10.1 shows how to calculate the gradients with autodiff for linear_graph.

  1. Start with call_with_info() which returns the the call site information, fwd_call_info.

  2. Then, calculate the information for the gradient graph, bwd_graph_info, by applying autodiff() to linear_graph.

  3. Next, get all the activations calculated in the forward pass with the gradient graph using bwd_graph_info.inputs_dict() with fwd_call_info as input.

  4. Last, calculate the gradient graphs with call(). grad_seed is the initial value of the partial gradient. Increasing grad_seed can serve as loss scaling. activation is used to connect the input of the gradient graph with the caller graph.

Listing 10.1 Example of calculating gradients with autodiff
18class Linear(popxl.Module):
19    def __init__(self):
20        self.W: popxl.Tensor = None
21        self.b: popxl.Tensor = None
22
23    def build(
24        self, x: popxl.Tensor, out_features: int, bias: bool = True
25    ) -> Tuple[popxl.Tensor, ...]:
26        self.W = popxl.graph_input((x.shape[-1], out_features), popxl.float32, "W")
27        y = x @ self.W
28        if bias:
29            self.b = popxl.graph_input((out_features,), popxl.float32, "b")
30            y = y + self.b
31        return y
32
33
34with main:
35    # host load
36    input = popxl.h2d_stream([2, 2], popxl.float32, name="input_stream")
37    x = ops.host_load(input, "x")
38    W_data = np.random.normal(0, 0.1, (2, 2)).astype(np.float32)
39    W = popxl.variable(W_data, name="W")
40    b_data = np.random.normal(0, 0.4, (2)).astype(np.float32)
41    b = popxl.variable(b_data, name="b")
42
43    # create graph
44    linear = Linear()
45    linear_graph = ir.create_graph(linear, x, out_features=2)
46
47    fwd_call_info = ops.call_with_info(
48        linear_graph, x, inputs_dict={linear.W: W, linear.b: b}
49    )
50    y = fwd_call_info.outputs[0]
51
52    # get the gradients from autodiff
53    bwd_graph_info = transforms.autodiff(linear_graph)
54    grad_seed = popxl.constant(np.ones((2, 2), np.float32))
55    activations = bwd_graph_info.inputs_dict(fwd_call_info)
56    grads_x, grads_w, grads_b = ops.call(
57        bwd_graph_info.graph, grad_seed, inputs_dict=activations
58    )
59
60    # host store
61    o_d2h = popxl.d2h_stream(y.shape, y.dtype, name="output_stream")
62    ops.host_store(o_d2h, y)
63
64    grad_d2h = popxl.d2h_stream(grads_w.shape, grads_w.dtype, name="grad_stream")
65    ops.host_store(grad_d2h, grads_w)

Download autodiff.py

The MNIST application example (Section 16, Application example: MNIST) demonstrates how autodiff is used.