15. Distributed PopXL Instances

15.1. Introduction

PopXL and the underlying Poplar SDK software stack are designed to help you run multiple instances of your single PopXL program in an SPMD (single program, multiple data) manner, for example with MPI. Combined with graph replication (see Section 14, Replication), each instance will have a “local” replication factor, and overall there will be a “global” replication factor. For example, you may wish to run your model in data-parallel across 16 replicas and 4 host instances. This means each instance will have a local replication factor of 4, and the global replication factor is 16. Global replication with no local replication is also possible. Each instance can only directly communicate with the replicas assigned to it, but is aware of the global situation (for example that it covers replicas 4…7 in a 4-instance program of 16 replicas total).

The reasons you may wish to distribute your replicas over multiple host instances include:

• To increase the potential bandwidth between host and IPU, by locating your instances on separate physical hosts (as each will have its own links to its IPUs).

• You must have at least one process per ILD when using a partition of IPUs that spans multiple ILDs. Please see here and here for more information on ILDs.

This concept is referred to as “multiple instances”, “multiple processes”, “multiple hosts”, “distributed instances”, “distributed replicated graphs”, and other similar terms.

15.2. Primer on using PopDist and PopRun to run multi-instance applications

You can use PopRun and PopDist to run multiple instances of your program using MPI. We will give a brief introduction here, but the PopDist and PopRun: User Guide contains more information.

PopDist provides a Python library that will help you set up a PopXL program to be run on multiple instances. Specifically, it will set metadata about the multi-instance environment (like global replication factor and which replicas are on the instance) in the session options, and will select a suitable device for the instance. PopDist gets this information from environment variables that are set for each process.

PopRun is a command-line interface that wraps your application command-line, and to which you pass options configuring the multi-instance setup, for example the number of instances, the hosts to spread the instances across, and the global replication factor. It can optionally create an appropriate V-IPU partition for you with the correct number of GCDs, devices, and so on, for running a Poplar program according to the multi-instance configuration you specified. It will then use MPI to run the command-line you passed according to this configuration. It can assign instances to the hosts in a NUMA-aware manner. The environment variables read by PopDist will be set appropriately in each instance for you. This enables PopDist to setup your PopXL program correctly on each instance.

15.3. Basic Example

This example shows how to configure a program to run on multiple instances using PopDist and PopRun.

Assume you have the following program model.py:

import popxl
ir = popxl.Ir()
with ir.main_graph:
  v = popxl.variable(1)
  w = popxl.variable(2)
  v += w
with popxl.Session(ir, 'ipu_hw') as sess:
  sess.run()
  print(sess.get_tensor_data(v))

To configure this program for multiple instances using PopDist, you only need to change the Ir-construction line to popxl.Ir(replication='popdist'). This will tell PopXL to use PopDist for configuring the session options and selecting the device.

The following poprun command runs your program model.py on 2 instances (--num_instances) with 2 global replicas (--num_replicas). This gives 1 replica per instance. It also creates an appropriate partition for you called popxl_test (--vipu-partition popxl_test --update-partition yes):

poprun \
  --vipu-partition popxl_test --update-partition yes \
  --num-replicas 2 --num-instances 2 \
  python model.py

If you pass --print-topology yes, PopRun will print a diagram visualising the topology it has created for you:

 ===================
|  poprun topology  |
|===================|
| hosts     |  [0]  |
|-----------|-------|
| ILDs      |   0   |
|-----------|-------|
| instances | 0 | 1 |
|-----------|-------|
| replicas  | 0 | 1 |
 -------------------

In a more realistic example, you would be doing something like data-parallel training over all of the global replicas. On each instance, the user would manage sending the right sub-batches of data to each instance in popxl.Session.run(). The optimiser step would perform an popxl.ops.replicated_all_reduce() on the gradient tensor before applying the optimiser step. The AllReduce will automatically happen across all the replicas across all the instances in an efficient way given the network topology between the replicas.

15.4. Variable ReplicaGroupings and multiple instances

Note

This section assumes you are familiar with using a ReplicaGrouping to control how a variable is initialised across replicas in PopXL. See Section 14.2, Replica grouping for more details.

The replica grouping is defined across the global replicas, not locally on each instance. This means that, in a multi-instance program, the default replica grouping of a single group containing all replicas is all of the replicas across all of the instances. This is what happened in the above example (it did not pass a replica grouping to popxl.variable so used the default): there was 1 group containing 2 replicas, and each instance had one of those replicas.

Therefore, groups can span across instances.

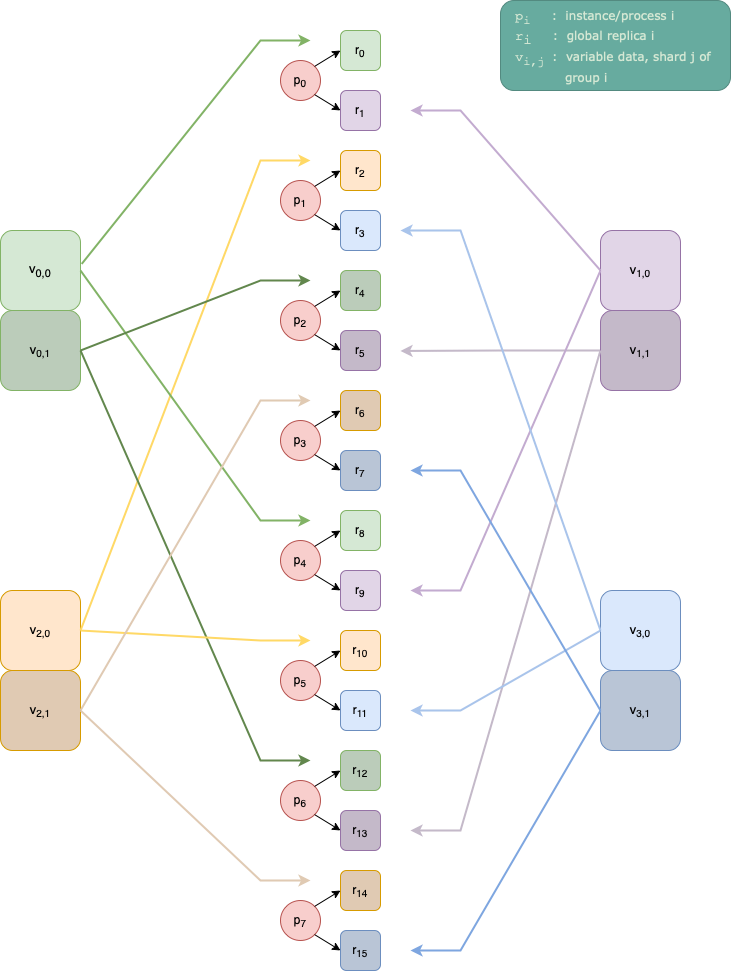
Fig. 15.1 shows a scenario for 2 instances a global replication factor of 2, and ReplicaGrouping(group_size=1, stride=1).

Fig. 15.1 The assignment of the replicas to instances, and the variable data from the host to each replica. This for 2 instances, 2 replicas, and ReplicaGrouping(group_size=1, stride=1).

As the variable has multiple groups, you must pass one set of host tensor data for each group. For a variable with shape shape and N groups (N > 1), this is done by passing host data of shape (N, *shape). In the example, there are 2 groups, so the host data you pass must have an extra dimension at the front of size 2.

For each replica, PopXL will send the data for that replica’s group to that replica. This happens as per usual in popxl.Session.weights_from_host(). In the above example, weights_from_host is called implicitly when entering the Session context. See Section 12, Session if you are unfamiliar with this.

Specifically, instance 0 will send w_data[0] to global replica 0 (which is local replica 0 on that instance); and instance 1 will send w_data[1] to global replica 1 (which is local replica 0 on that instance).

The code for such a program is shown in Listing 15.1.

Listing 15.1 Simple distributed example.

import numpy as np
import popxl

num_groups = 2
nelms_per_group = 4
host_shape = (num_groups, nelms_per_group)
v_data = np.arange(0, num_groups * nelms_per_group).reshape(host_shape)

ir = popxl.Ir(replication="popdist")
with ir.main_graph:
    grouping = ir.replica_grouping(group_size=1)
    v = popxl.variable(v_data, grouping=grouping)

    replica_shape = v.shape
    assert replica_shape == (nelms_per_group,)

    v += 1

with popxl.Session(ir, "ipu_hw") as sess:
    sess.run()
print(sess.get_tensor_data(v))

Download distributed_simple_example.py

You can print session.get_tensor_data(v) and see that every instance now has the full globally updated weight tensor. This is because, in popxl.Session.weights_to_host() (called implicitly on context exit in the above code), each instance will get their updated weight slices from their local replicas, then communicate the data between them so all instances have all the updated data.

The program above is what each instance executes in an SPMD paradigm (using MPI, if using PopRun). However, the code is aware of the full global picture. That is, each instance running the code is passing a replica grouping defined over the global replica space; each passes the full global v_data even though some of the data will not belong to the replicas of that instance; and each returns the full global data in session.get_tensor_data(v).

15.4.1. Detail of inter-instance communication

In weights_to_host, each instance will send the data from each local replica to the same corresponding slice in the weight’s data buffer. We are using the default one_per_group variable retrieval mode, so we only send data from the first replica in each group back to host (see parameter retrieval_mode of popxl.variable()).

At this point, each instance has updated the slices of the host weight buffer only for the groups whose first replica resided on that instance. Thus, the instances need to communicate with each other to recover the fully updated weight tensor.

Let us examine the example in Listing 15.1. There are 2 groups. The first replica of group 0 is global replica 0, which is local replica 0 on instance 0. Therefore, instance 0 will fetch the updated v data from that replica and write it to the internal host buffer for group 0 of v.

The first replica of group 1 is global replica 1, which is local replica 0 on instance 1. Therefore, instance 1 will fetch the updated v data from that replica and write it to the internal host buffer for group 1 of v.

At this point, instance 0 has only updated the data for group 0 locally, and instance 1 has only updated the data for group 1 locally. The instances will therefore communicate between themselves so that all instances have all the updated data. PopXL does all of this automatically.

Say we had used variable retrieval mode all_replicas (see parameter retrieval_mode of popxl.variable()). The host buffer would hold one weight tensor value per global replica, but each instance will have only updated it for the replicas that reside on that instance. As with the above case, the instances will automatically communicate to recover the full weight tensor.

Internally, PopXL uses MPI for performing the inter-instance communication, and will automatically initialise an MPI environment for you.

15.5. Sharding and multiple instances

Note

This section assumes you are familiar with replicated tensor sharding (RTS) in PopXL. See Section 13.3, Variable tensors for replicated tensor sharding for more information.

Sharding is supported on multiple instances using the same APIs as for single instance programs.

15.5.1. Basic Example

Like with replica groupings, the sharding is defined over the global replicas.

Going back to the example of 2 instances, 2 global replicas, and 1 group of size 2. The default sharding (which is to shard across every replica in the group) would result in the first shard of the weight data going to the first global replica, and the second shard going to the second global replica. As replica 0 is on instance 0, instance 0 will send the corresponding shard to that replica. Similarly for replica 1 and instance 1. In weights_to_host, the instances will each retrieve the shard from their local replica, then communicate with the other instance to reconstruct the full updated weight tensor on that instance.

Such a program is shown in Listing 15.2.

Listing 15.2 Simple distributed RTS example.

ir = popxl.Ir(replication="popdist")
with ir.main_graph:
    v_handle, v_shard = popxl.replica_sharded_variable([1, 1])
    # v_shard will be [1] on each replica

    # Dummy RTS forward pass: gather your shards and perform some ops.
    v_gathered = ops.collectives.replicated_all_gather(v_shard)
    w = popxl.variable([2, 2])
    ops.matmul_(w, v_gathered)

    # Dummy RTS backward pass: you have gradients for the whole v,
    # reduce-scatter them then perform the optimiser step on your shard.
    v_grad = popxl.constant([1, 1])
    v_grad_shard = ops.collectives.replicated_reduce_scatter(v_grad)
    v_shard += v_grad_shard
    # v_shard is now [2] on each replica.

with popxl.Session(ir, "ipu_hw") as sess:
    sess.run()
    print(sess.get_tensor_data(v_handle))
    # -> [2, 2]   <- The full updated tensor reconstructed from all shards

Download distributed_rts_simple_example.py

Note we do not need to explicitly pass the replica_grouping or shard_over parameters to popxl.replica_sharded_variable as we are using the default settings of 1 group and sharding across every member of that group.

As before, each instance passes the full global tensor data to PopXL, and the full global data is returned.

Listing 15.3 shows the same example, but instead of using popxl.replica_sharded_variable, we manually create a remote buffer and manually load from and store to it. If you are unfamiliar with the RTS API, please refer to Section 13.3, Variable tensors for replicated tensor sharding.

Listing 15.3 Simple distributed RTS example with manual control of the remote buffer.

ir = popxl.Ir(replication="popdist")
with ir.main_graph:
    remote_buffer = popxl.replica_sharded_buffer((2,), popxl.dtypes.int)
    v_handle = popxl.remote_replica_sharded_variable([1, 1], 0, remote_buffer)
    v_shard = ops.remote_load(remote_buffer, 0)
    # v_shard will be [1] on each replica

    # Dummy RTS forward pass: gather your shards and perform some ops.
    v_gathered = ops.collectives.replicated_all_gather(v_shard)
    w = popxl.variable([2, 2])
    ops.matmul_(w, v_gathered)

    # Dummy RTS backward pass: you have gradients for the whole v,
    # reduce-scatter them then perform the optimiser step on your shard.
    v_grad = popxl.constant([1, 1])
    v_grad_shard = ops.collectives.replicated_reduce_scatter(v_grad)
    v_shard += v_grad_shard
    # v_shard is now [2] on each replica.

    ops.remote_store(v_shard, remote_buffer, 0)

with popxl.Session(ir, "ipu_hw") as sess:
    sess.run()
    print(sess.get_tensor_data(v_handle))
    # -> [2, 2]   <- The full updated tensor reconstructed from all shards

Download distributed_rts_simple_example_manual_remote_buffer.py

We have replaced one call to popxl.replica_sharded_variable with popxl.replica_sharded_buffer to create a remote buffer with a tensor shape equivalent to the shape of one shard; popxl.remote_replica_sharded_variable to create the remote variable handle; and ops.remote_load / ops.remote_store to load/store the shard from the remote buffer.

Note, we pass the full global unsharded shape to popxl.replica_sharded_buffer.

15.5.2. Using shard_over

You can use the shard_over parameter to specify the number of replicas in a group that the weight is sharded over (see popxl.replica_sharded_buffer() or popxl.replica_sharded_variable()). The weight will be repeatedly sharded over every shard_over consecutive replicas of the group. For example, for w = [1, 2], 4 replicas in the group, and shard_over=2, the replicas will get the values:

Replica 0: [1]
Replica 1: [2]
Replica 2: [1]
Replica 3: [2]

The same thing happens when this is a multi-instance program and these are the global replicas spread across instances. For example, if there were 2 instances, replicas 0 and 1 would be on instance 0, and replicas 2 and 3 would be on instance 1. Each instance would send the correct slices of the weight data to each of its local replicas based on the replica grouping and sharding settings.

15.5.3. Complex Example

Let us now consider a more complex example, with 8 instances, 16 global replicas, ReplicaGrouping(group_size=4, stride=4), and shard_over=2. This is shown in Fig. 15.2.

Fig. 15.2 The assignment of the replicas to instances, and of the variable data from the host to each replica. This for 8 instances, 16 replicas, ReplicaGrouping(group_size=4, stride=4) and shard_over=2.

We will write a rather contrived, arbitrary program as a minimal example of using such settings. The program creates the variable with these settings, AllGathers the shards, performs an inplace element-wise addition, scatters the result across replicas, and updates the shards to be those values. This program is shown in Listing 15.4.

Listing 15.4 Distributed RTS example with ReplicaGrouping(group_size=4, stride=4) and shard_over=2.

ir = popxl.Ir(replication="popdist")

# Should be 16 in our scenario.
rf = ir.replication_factor
rg = ir.replica_grouping(group_size=4, stride=4)
# 4
num_groups = rg.num_groups
# Shard over half the group, so in this case 2
shard_over = num_groups // 2
# Let (32,) be shape of unsharded v, and we need 4 groups worth of data
v_h = np.arange(0, num_groups * 32).reshape((num_groups, 32))

with ir.main_graph:
    v_handle, v_shard = popxl.replica_sharded_variable(
        v_h, replica_grouping=rg, shard_over=shard_over
    )

    collective_rg = ir.replica_grouping(
        group_size=rg.group_size // shard_over, stride=rg.stride
    )
    v_gathered = ops.collectives.replicated_all_gather(v_shard, collective_rg)

    v_gathered += 1

    v_updated_shard = ops.collectives.replica_sharded_slice(v_gathered, collective_rg)

    ops.var_updates.copy_var_update_(v_shard, v_updated_shard)

with popxl.Session(ir, "ipu_hw") as sess:
    sess.run()
    print(sess.get_tensor_data(v_handle))
    # Will print the full updated tensor reconstructed from all shards.
    # This will be equivalent to `v_h + 1`.

Download distributed_rts_complex_example.py

To run this program on 16 replicas and 8 instances using PopRun:

poprun \
  --vipu-partition popxl_test --update-partition yes \
  --num-replicas 16 --num-instances 8 \
  python model.py

Note, when we create the variable, we describe what replicas will get what data through a combination of both replica_grouping and shard_over. We think of it as 4 groups each repeatedly sharding their value over every 2 replicas in that group. However, when we perform the collective and pass a replica grouping to describe what combinations of replicas should gather with each other, there is only the one replica_grouping parameter and we have to construct the appropriate grouping for gathering the shards manually. The grouping we need is the original grouping, but with the group_size divided by the shard_over. This is done in the highlighted lines of the example.

The reason the API is like this is because, conceptually, the APIs for describing how to initialise a variable across replicas and which replicas collectives should be performed across have no bearing on each other, they just both happen to use replica groupings for describing groups of replicas.

Warning

However, when AllGather-ing a sharded tensor, the replica grouping that is exactly the grouping used to initialise the variable with the group size divided by the shard over, is the only replica grouping that is valid. This is because the data for the shards you are gathering comes from the variable’s host data, and this data was CBR-rearranged before being split into shards and uploaded to each device. Therefore, unless the sharding configuration of the variable and the replica grouping of the AllGather are exactly semantically equivalent, the AllGather will not know how to undo the CBR-rearragement on its output tensor. If you attempt to pass any other replica grouping, it is undefined behaviour.

For any replicated collective other than AllGather, or if the input tensor of the AllGather is not a sharded tensor, you can pass any replica grouping you want, even if the input tensor is a variable that was initialised using a different replica grouping.